Video: Koks yra geriausias sujungimo rūšiavimo atvejo laiko sudėtingumas?
2024 Autorius: Lynn Donovan | [email protected]. Paskutinį kartą keistas: 2023-12-15 23:50
Rūšiavimo algoritmai
| Algoritmas | Duomenų struktūra | Erdvės sudėtingumas: blogiausias |
|---|---|---|
| Greitas rūšiavimas | Masyvas | O(n) |
| Sujungti rūšiavimą | Masyvas | O(n) |
| Krūvos rūšiavimas | Masyvas | O(1) |
| Lygus rūšiavimas | Masyvas | O(1) |
Be to, koks yra sujungimo rūšiavimo laiko sudėtingumas?
The sujungimo rūšiavimo sudėtingumas yra O(nlogn) ir NE O(logn). Padalinimo žingsnis apskaičiuoja kiekvieno pomasyvo vidurio tašką. Kiekvienas iš šio žingsnio trunka tik O (1) laikas . Užkariavimo žingsnis rekursyviai rūšių po du n/2 (lyginių n) elementų posistemius.
koks yra geriausias burbulų rūšiavimo sudėtingumas? Kosmosas sudėtingumo dėl Burbulų rūšiavimas yra O(1), nes reikia tik vienos papildomos atminties vietos, t. y. temp kintamajam. Taip pat, geriausiu atveju laiko sudėtingumas bus O(n), tai yra tada, kai sąrašas jau yra surūšiuoti.
Be to, koks yra geriausias sujungimo rūšiavimo atvejis?
n*log(n)
Koks yra įterpimo rūšiavimo sudėtingumas geriausiu ir blogiausiu atveju?
Geriausia , Blogiausias , ir vidutinis atvejų The geriausiu atveju įvestis yra masyvas, kuris jau yra surūšiuoti . Šiame atvejo įterpimo rūšiavimas turi linijinį veikimo laikas (t. y. O(n)). Kiekvienos iteracijos metu pirmasis likęs įvesties elementas lyginamas tik su labiausiai dešiniuoju esančiu elementu surūšiuoti masyvo poskyris.
Rekomenduojamas:
Kuris rūšiavimo algoritmas yra geriausias blogiausiu atveju?
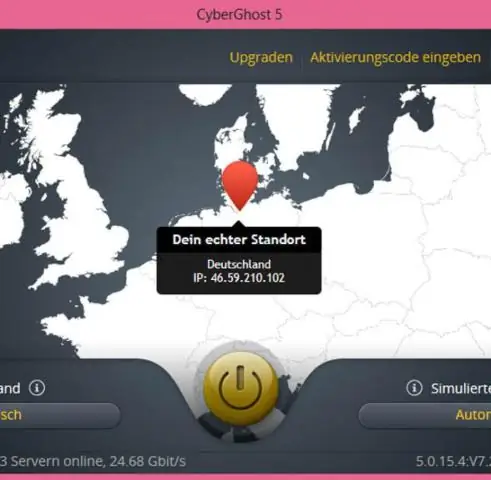
Rūšiavimo algoritmai Algoritmas Duomenų struktūra Laiko sudėtingumas: Blogiausias Greitas rūšiavimas Masyvas O(n2) Sujungti rūšiavimas Masyvas O(n log(n)) Krūvos rūšiavimas Masyvas O(n log(n)) Sklandus rūšiavimas Masyvas O(n log(n))
Kaip apskaičiuojamas sujungimo rūšiavimo sudėtingumas?
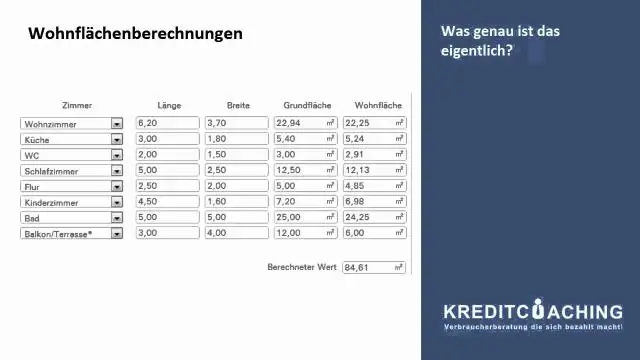
2 atsakymai. Mazgo A[L,R] padalijimas į du mazgus užtrunka R&minus L+1 laiką, o tada sujungiant du antrinius mazgus A[L,M] ir A[M+1,R] vėl reikia A[R−L +1] kartą. Taigi kiekvienam mazgui algoritmo atliekamų operacijų skaičius yra lygus dvigubam masyvo, atitinkančio tą mazgą, dydžiui
Koks yra krūvos rūšiavimo algoritmo sudėtingumas?
Krūvos rūšiavimas yra algoritmas vietoje. Laiko sudėtingumas: Heapify laiko sudėtingumas yra O(Logn). CreateAndBuildHeap() laiko sudėtingumas yra O(n), o bendras krūvos rūšiavimo laiko sudėtingumas yra O(nLogn)
Koks yra krūvos stūmimo operacijos laiko sudėtingumas?
Visų standartinių dėklo operacijų (push, pop, isEmpty, size) atveju blogiausio atvejo vykdymo laiko sudėtingumas gali būti O(1). Sakome, kad galima ir ne, nes visada galima įdiegti stekelius su pagrindiniu vaizdu, kuris yra neefektyvus
Kas yra laiko sudėtingumas duomenų struktūroje?
Algoritmo laiko sudėtingumas kiekybiškai įvertina laiką, per kurį algoritmas veikia, kaip įvesties ilgio funkciją. Panašiai algoritmo erdvės sudėtingumas kiekybiškai įvertina vietos arba atminties kiekį, kurio algoritmas paleidžia, kaip įvesties ilgio funkciją